1° ENIGMA: COMPLETA LA SERIE
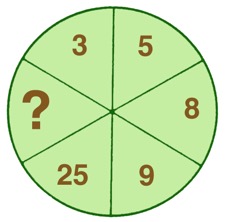
Trova il numero che completa la serie.
SOLUZIONE
64
Nel semicerchio inferiore sinistro si trovano i quadrati dei numeri loro opposti nel semicerchio superiore destro.
2° ENIGMA: ADDIZIONI IN CODICE
Nella tabella seguente, sono state eseguite addizioni sia in orizzontale sia in verticale. Ciascuna delle figure (il cerchio rosso, la stella viola, il rombo verde, il quadrato marrone e la mela blu) sostituisce sempre uno stesso un numero.
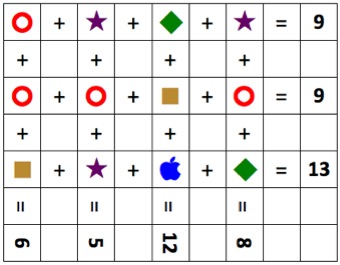
Ovviamente due simboli differenti rappresentano due numeri differenti.
Trova quali sono i numeri da mettere al posto delle figure affinché tutte le addizioni siano giuste.
A quale numero corrisponde il rombo verde?
Quale valore ha la mela blu?
SOLUZIONE
Il rombo verde vale 4. La mela blu vale 8.
Si può procedere per tentativi attribuendo dei valori ai diversi simboli, effettuare le addizioni e confrontare i risultati con i numeri scritti alla fine delle righe e delle colonne.
Meglio ancora è però osservare che l'unica differenza tra la prima colonna e la seconda riga è il cerchio rosso, da cui il suo valore: 9 - 6 = 3.
Nello stesso modo si trova il rombo verde come differenza tra la prima riga e la seconda colonna, dunque 4.
Si trova la stella confrontando la terza riga e la terza colonna e poi il quadrato togliendo alla seconda riga tre cerchi.
Per finire, la mela blu sarà calcolata nella terza colonna.
Oppure procedere per ipotesi e deduzioni. Per esempio, attribuire il valore 1 al cerchio e dedurre, utilizzando la prima colonna, che il quadrato vale allora 4. Sostituire il cerchio con 1 e il quadrato con 4 nella seconda riga e verificare che la somma non è 9.
Ricominciare quindi con un altro valore per il cerchio. Arrivare infine alla soluzione: cerchio rosso: 3, quadrato marrone: 0, stella viola: 1, rombo verde: 4, mela blu: 8.

Il papà di Luca ha costruito un tavolo rettangolare da giardino utilizzando 7 assi di legno uguali, ciascuna di perimetro 3 metri.
Ecco il disegno del piano del tavolo così come appare al termine del lavoro.
Quali sono la lunghezza e la larghezza di questo tavolo da giardino?
SOLUZIONE
Larghezza 125 cm (1,25 m) e lunghezza 175 cm (1,75m)
Dalla disposizione delle assi all’interno del piano del tavolo si capisce che la lunghezza di un’asse è 5 volte la sua larghezza e che quindi il suo perimetro è 12 volte tale larghezza (2x5+2x1). Ne segue che la larghezza di un’asse è 25 cm (300:12).
Di conseguenza, essendo la larghezza e la lunghezza del piano del tavolo, rispettivamente, 5 e 7 volte la larghezza di un’asse, le dimensioni del tavolo sono 125 cm (25x5) e 175 cm (25x7).
Oppure: si può notare sul disegno che il perimetro del piano del tavolo può esprimersi per mezzo dei lati di un’asse poiché è formato da 4 larghezze e 4 lunghezze.
Ne segue che il perimetro del piano del tavolo è 2 volte quello di un’asse, cioè 600 cm (300x2).
Notare poi che la lunghezza di un’asse è 5 volte la sua larghezza e che quindi il perimetro del piano del tavolo corrisponde a 24 volte la larghezza di un’asse; dedurne che (600:24)x5=125 cm è la larghezza del tavolo, mentre la lunghezza è (600:24)x7 = 175 cm.



