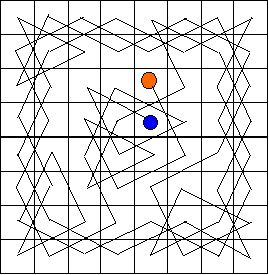
Si tratta di trovare un percorso che porti il cavallo ad occupare tutte le caselle della scacchiera partendo da una casella qualsiasi e passando una e una sola volta su ogni altra casella.
Se la casella di partenza e quella di arrivo sono ancora unite fra loro dalla mossa del cavallo, il viaggio di dice "chiuso", altrimenti è "aperto".
Un primo aiuto per risolvere il problema può venire dal consiglio del matematico francese De Moivre, noto per i suoi studi sul calcolo delle probabilità: si cerchi di occupare prima la fascia esterna delle caselle della scacchiera, senza entrare, salvo i casi di assoluta necessità, nel quadrato centrale 4 x 4 e si proceda sempre nello stesso verso.
Solo quando tutte le caselle della fascia esterna saranno occupate, si passerà a quelle centrali.
Nella figura sopra riportiamo una soluzione del problema, un viaggio "aperto", ma con uno schema particolarmente elegante, proposto da Dudeney.
Eulero, il grande matematico svizzero, propose nel Settecento, una strategia di gioco che consente di porre rimedio ad eventuali errori, recuperando caselle che siano rimaste fuori dal percorso, non più raggiungibili dal cavallo, purché queste non siano più di quattro.
Vediamo il suo procedimento su un esempio.
Si parte da una casella qualsiasi e si prosegue, sempre con la mossa del cavallo, finché non c'è più possibilità di movimento.
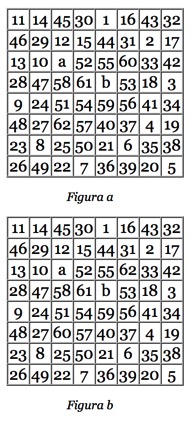
Nel nostro esempio di figura (a), restano scoperte le caselle a e b.
Per prima cosa, chiudiamo il "viaggio" collegando la prima casella, la 1, all'ultima la 62.
Per far questo dobbiamo scegliere tra le caselle "attaccate" dal cavallo in posizione 1 e 62, due caselle consecutive, la cui differenza sia perciò uguale a 1.
In questo caso, la casella 1 attacca le caselle 60, 2, 12 e 52, mentre la 62 attacca le caselle 21, 59, 61, 47, 9, 23, 49 e 7.
Sono quindi le caselle 60 e 59 che ci permettono di chiudere il viaggio. Infatti la successione 1 - 2 - 3 - … - 59 e 62 - 61 - 60 corrisponde a un viaggio chiuso.
E' sufficiente, figura b) sostituire la sequenza 62 - 61 - 60 con 60 - 61 - 62 per avere le mosse in ordine.
Se la prima e l'ultima casella non fossero collegate da due caselle consecutive, si dovrebbero cercare altre caselle, con numeri intermedi, che soddisfino questa condizione, in modo da modificare il percorso per arrivare sempre alla fine con la prima e l'ultima casella collegate fra loro.
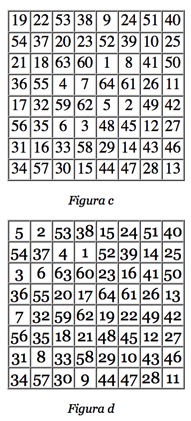
Non dimentichiamoci però delle caselle a e b, che sono ancora fuori dal percorso.
Vediamo come inserire la casella a.
Questa casella attacca le caselle 54, b, 44, 30, 14, 46, 28 e 24.
Se riusciamo a mettere una di queste caselle all'ultimo posto del percorso, cioè alla casella 62, potremmo aggiungere con un nuovo salto la casella a (e in questo caso anche la b che in questo caso è già collegata alla a dalla mossa del cavallo).
Scegliamo per questo una qualsiasi delle caselle attaccate dalla a, ad esempio la 54 che può diventare la sessantaduesima aggiungendo 8.
Dobbiamo aggiungere naturalmente 8 a tutte le altre caselle, con l'avvertenza di sostituire 63, 64, 65, 66, 67, 68, 69 e 70 con 1, 2, 3, 4, 5, 6, 7 e 8.
A questo punto il viaggio è completo, figura c), ma aperto.
Per chiudere il percorso ripetiamo il procedimento che abbiamo appena visto sulle caselle 24 e 23, che collegano fra loro la prima e l'ultima casella, e otteniamo il percorso chiuso di figura d).
Per saperne di più
Italo Ghersi, Matematica dilettevole e curiosa, Hoepli, 1978, pp. 74 - 84.
Fred Schuh, The master book of mathematical recreations, Dover, 1968, pp. 349 - 354.
La pagina di Mathworld dedicata al Viaggio del cavallo: http://mathworld.wolfram.com/KnightsTour.html
Il Viaggio del cavallo secondo la teoria dei grafi: http://space.tin.it/scuola/vdepetr/t18/Text18.htm
Saggi suThe knight's tour: http://www.ktn.freeuk.com/index.htm
L'analisi del gioco di Ed Pegg Jr.: http://www.mathpuzzle.com/leapers.htm
Il Teorema di Schwenk per il Viaggio del cavallo e la presentazione del gioco: http://en.wikipedia.org/wiki/Knight's_tour
Il Viaggio del cavallo di F. Friedel: http://www.chessbase.com/columns/column.asp?pid=163
La tecnica per il Viaggio del cavallo: http://www.memorymentor.com/knight.htm
Applet Java del Viaggio del cavallo: http://members.tripod.com/vpdesai/ktour.htm e anche http://www.borderschess.org/KnightTour.htm
Una completa sitigrafia: http://www.velucchi.it/mathchess/knight.htm

