E LA MISURA DELLA CIRCONFERENZA TERRESTRE
Non sempre si riesce, nell'insegnamento della matematica, a trovare situazioni problematiche reali che introducano le tecniche di calcolo da studiare. Un esempio può essere questo classico problema: come fecero gli antichi scienziati a calcolare la grandezza della Terra?
Collocazione storica e geografica
Eratostene vive nel III secolo a.C., studia ad Atene e successivamente si trasferisce ad Alessandria per dirigere la più grande biblioteca fino allora mai esistita. La città di Alessandria era stata fondata da Alessandro Magno che aveva esteso i territori greci conquistando un immenso impero e contestualmente aveva posto le basi per l'espansione della cultura greca. Proprio ad Alessandria la cultura scientifica greca raggiunge livelli elevatissimi.
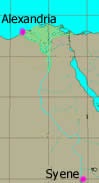
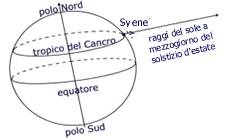
Il fatto si svolge tra Alessandria, che si trova alla foce del Nilo e l'attuale Assuan, allora chiamata Syene. I due luoghi si trovano in una posizione geografica che è cruciale per l'esperienza in questione: Syene si trova "quasi' sul Tropico del Cancro e Alessandria si trova a nord di Syene, "quasi" sullo stesso meridiano terrestre.
Il problema
Era già noto che la Terra avesse una forma sferica. Una tale convinzione derivava dal fatto che durante le eclissi di Luna, la forma dell'ombra terrestre appare sempre come un arco di circonferenza.
Il problema più stimolante non era quello qualitativo di accertarne la forma ma quello quantitativo di misurarne la grandezza. In altre parole assodato che la Terra ha una forma sferica quanto misura la sua circonferenza? Come si poteva misurare questa grandezza se le distanze in gioco erano enormi per quei tempi e gli oceani costituivano un ostacolo insormontabile?
La strumentazione tecnica
Lo strumento di cui si serve Eratostene è incredibilmente semplice, un banale bastone piantato verticalmente in un terreno perfettamente pianeggiante: lo gnomone. Studiando l'ombra che si genera si possono seguire i movimenti del Sole. Durante il giorno, il momento in cui l'ombra è più corta corrisponde a mezzogiorno.
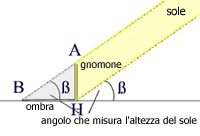
Lo gnomone permette di seguire anche il cambio delle stagioni: il giorno in cui a mezzogiorno l'ombra è più corta è il solstizio d'estate; sei mesi dopo, l'ombra a mezzogiorno è la più lunga ed è il solstizio d'inverno. Infine si può stabilire in ogni momento l'altezza del Sole, ossia l'angolo ß che i suoi raggi formano con la linea dell'orizzonte, confrontando semplicemente la lunghezza del bastone AH con la sua ombra BH.
Nella città di Syene, il giorno del solstizio d'estate, a mezzogiorno, il bastone non dà ombra, il che significa che i raggi del Sole cadono perpendicolarmente al terreno: il Sole si dice che è allo zenit.
L'argomentazione
A mezzogiorno d'estate Eratostene misura l'altezza del Sole nella città di Alessandria. Poiché sa che in quel momento il Sole è perfettamente perpendicolare a Syene, ottiene l'angolo tra la verticale ad Alessandria e la verticale a Syene. Questo angolo è esattamente quello formato dal raggio della Terra che ha per estremo Alessandria e dal raggio che ha per estremo Syene.

L'angolo a risulta essere 1/50 dell'intera circonferenza, in gradi 7° e 12' (cioè 7,2°).
Eratostene, quindi, scrive la proporzione
l : C = a : 360° cioé --> 5.000 : C = 7,2° : 360°
e ottiene
C = (l x 360°) : a = (5000 x 360°) : 7,2° = 250 000 stadi
(circa 40.000 km ... un valore incredibilmente vicino a quello reale di 40.009 km ... che è la lunghezza della circonferenza del meridiano terrestre).
Congetture nascoste
Questa argomentazione richiede in realtà l'assunzione di altre ipotesi: che la Terra sia perfettamente sferica, che il Sole sia così distante dalla Terra da poter considerare paralleli i raggi del Sole ad Alessandria con quelli a Syene, che le due città siano esattamente sullo stesso meridiano terrestre, che sia possibile misurare correttamente la distanza tra le due città.
Bibliografia
R.Osserman, Poesia dell'universo. L'esplorazione matematica del cosmo, Longanesi & C., Milano, 1996.
L.Russo, La rivoluzione dimenticata. Il pensiero scientifico greco e la scienza moderna, Feltrinelli, Milano 1996.
